Coordinate Systems
A coordinate system is a method to define the unique position on a plane or in space of geometric elements using combinations of numbers called coordinates. There are two types of Earth coordinate systems: geographic and projected.
Our company is named after René Descartes, the inventor of the cartesian coordinate system in the 17th century. This coordinate system was the first link between geometry and algebra, and the foundation for projected coordinate systems.
Geographic coordinate systems Geographic coordinates are perhaps the most familiar way of representing coordinates on the Earth’s surface. In these coordinates systems, a location is represented by its latitude (north-south position) and longitude (east-west position). Latitude and longitude are defined using an ellipsoidal representation of the Earth. Because the coordinates are defined on a curved surface, the physical distance covered by one degree of longitude will vary from north to south (due to convergence at the poles), as will latitude from east to west (due to the ellipsoid shape). Placing coordinates on a flat surface requires a map projection, described in the next section.
Map projections and projected coordinate systems For many practical purposes, we need to project coordinates onto a 2D plane. A projected coordinate system is defined on a flat, two-dimensional surface. Projected coordinate systems describe locations in linear units (such as meters or feet).
Since map projection are abstractions of a 3D Earth onto a 2D plane, distortions are inevitable. These distortions differ for each map projection but are well known and studied. Distortions that can occur with a flat map include those related to: - shape - area - distance - direction
While it is impossible to maintain all the native spatial elements of your geometries once projected, you can prioritize the most important element for your maps purpose. Projections often use descriptive names like “conformal”, “equidistant”, “equal-area”, and “azimuthal” to describe the properties that they preserve. A projection can accurately preserve one property (either shape, area, distance or direction) but not others. For this reason, it’s important to choose a projection that preserves the properties that are relevant to your application. For example, the Mercator projection is used for navigation because it preserves the angle between any two curves (conformal projection).
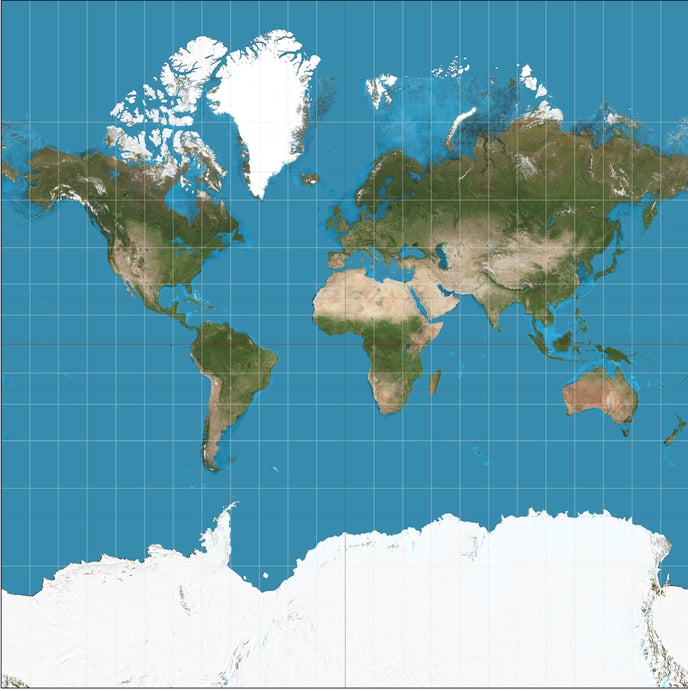
Mercator Distortion: The Mercator projection is area distorting, resulting in land masses near the poles to appear much larger relative to those at the equator.
